剑指 Offer 68 - II. 二叉树的最近公共祖先

题目描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（ 一个节点也可以是它自己的祖先 ）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

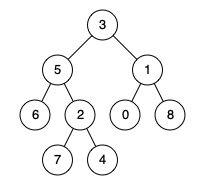
示例 1:

1
2
3

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

1
2
3

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。

注意：本题与主站 236 题相同：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/

算法

(递归) $O(n)$

求公共祖先需要自底向上递归遍历二叉树，那么可以按照后序顺序遍历。

题目已知 $p$ 和 $q$ 一定在二叉树中，所以一定存在非空答案。

递归三部曲：

递归函数的含义：直接使用题目给出的函数，返回以 $root$ 为根节点二叉树中节点 $p$ 和 $q$ 的最近公共祖先，返回值就是最近公共祖先。返回值总共有四种情况：
- 如果以 root 为根的子树中包含 p 和 q，则返回它们的最近公共祖先即 root
- 如果只包含 p，返回 p
- 如果只包含 q，返回 q
- 如果都不包含，则返回 NULL
递归出口条件：如果当前节点 $root$ 为空或等于 $p$ 或等于 $q$，直接返回当前节点即可。
- 如果 root == NULL 说明没找到 p 或 q，返回 NULL 即可
- 如果 root == p 说明当前树包含 p，p 是它自己的最近公共祖先，返回 p
- 如果 root == q 说明当前树包含 q，q 是它自己的最近公共祖先，返回 q
单层递归逻辑：递归查找左子树中 $p$ 和 $q$ 的最近公共祖先 $left$，递归查找右子树中 $p$ 和 $q$ 的最近公共祖先 $right$，所以对于 $left$ 和 $right$ 有四种情况：
- 如果 $left$ 为空，最近公共祖先一定在右子树中，返回 $right$ 即可。
- 如果 $right$ 为空，最近公共祖先一定在左子树中，返回 $left$ 即可。
- 如果 $left$ 和 $right$ 都不为空，则返回当前节点
- 如果 $left$ 和 $right$ 都为空，则返回空，这种情况可以在第一种情况中得到处理。

时间复杂度

二叉树中的每个节点只需被遍历一次，所以时间复杂度为 $O(n)$。

空间复杂度

最坏情况下二叉树呈链状，需要 $O(n)$ 的空间。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (p == root || q == root || !root) return root;
        auto left = lowestCommonAncestor(root->left, p, q);
        auto right = lowestCommonAncestor(root->right, p, q);
        if (!left) return right;
        if (!right) return left;
        return root;
    }
};